Astrolabe Trigonometry-Sine Quadrants
İBRAHİM AYBEK
2024-LISBON
HOW TO CONVERT ROOT NUMBERS TO APROXIMATE FRACTIONAL NUMBERS BY ASTROLABE
Astrolabes are sophisticated devices used mainly between 8th to 19th century in the world by astronomers and geographers in history. Beside its several functions related to time calculations it was also used as a trigonometrical calculator by its sine quadrant which was most of the times located on the back side of astrolabe. Sine quadrants are basicly checked charters as we use today in may notebooks for studens. Let see what we are talking about.
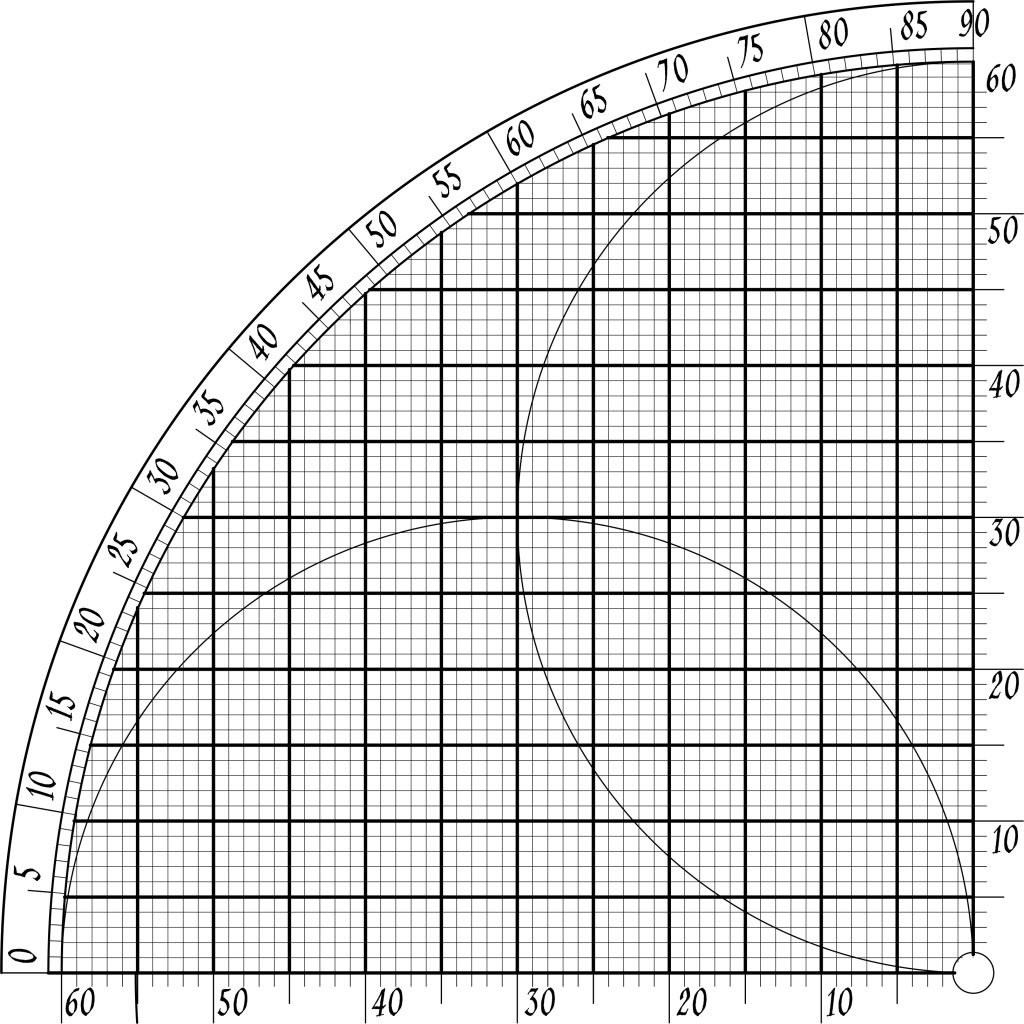
Islamic scholars most of the times divided a quarter of circle in 60 parts instead of 100. Because 60 can be divided in 2,3,4,5,6,8,10,12,15 and 30 while 100 can be divided only by 2,4,5,10,25 and 50. That’s wht using 60 square unit was more practical than 100 units to quickly proportion measurements.
In the past this chart were used mainly used to calculate shadow lenght or calculate distance to determinate object like mountains, buildings, or horizont. Lets see a sample calculation made by using trigonometrical functions of sine quadrant.
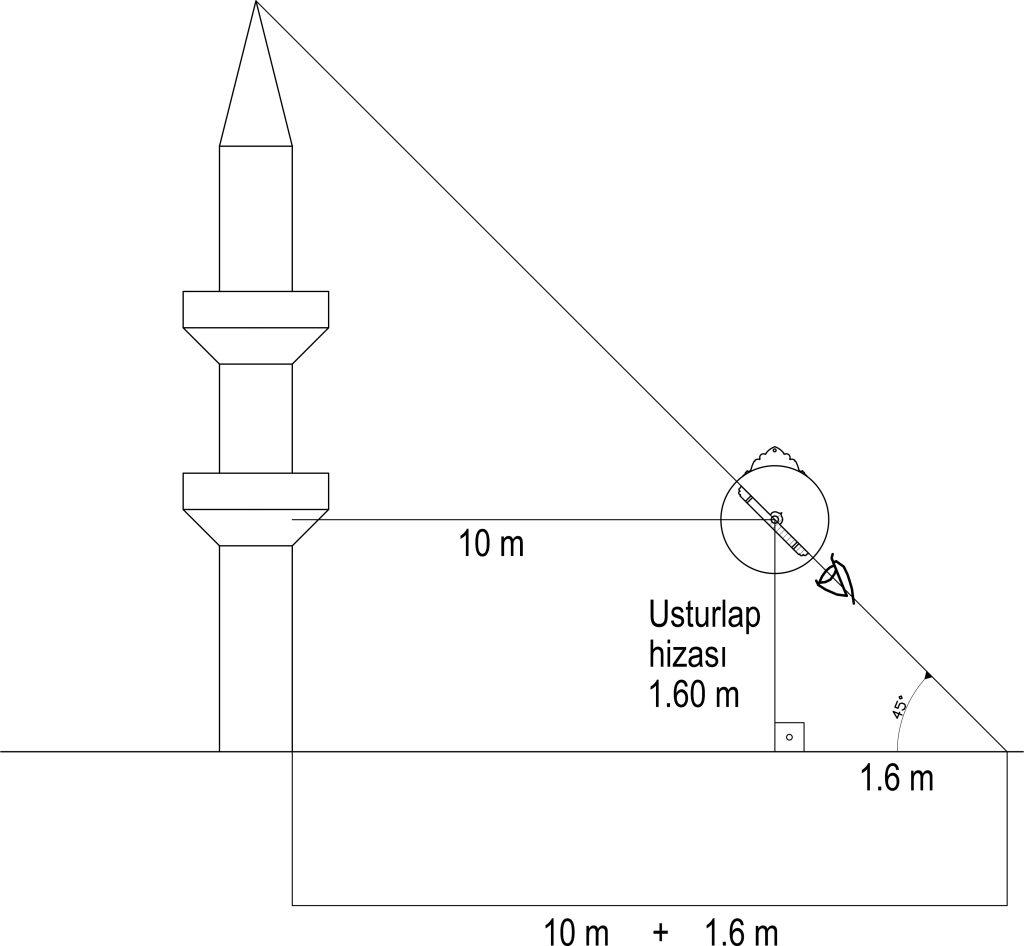
| Ex.1: Finding the Height of a Minaret |
After adjusting the astrolabe to 45° in order to measure the height of the minaret, the observer, who moves away from the minaret by aiming at the top of the minaret, measures his distance from the minaret as 10 m. When the person measures, they’ll measure the height of the astrolabe as 1.6 m.
According to the diagram below, the height of the minaret is 11.60 meters.
As you can see in the example measurer uses sine value of observed angle to calculate elevation of some object which he can calculate its shadow on ground easier than measuring an elevated building. This example shows us sine quadrants were giving trigonometrical values of any angle converted to aproximate fractional numbers. Thtough Pytagorian geometry we can get this values easily but we get root numbers instead of whole numbers which were not easy to convert in decimal numbers in the time. That’s why using root numbers were not serving to use them in practical calculations. Sine quadrants supply use these trigonometrical numbers converted to fractional numbers with very aproximate values, most of the times with less than %0,1 error margin.
Let’s see an example
Ex.2 Calculate trigonometrical values of 60 degrees.
In the picture, an angle of 30 degrees is drawn. The hypotenuse of this right triangle is 60 units. The opposite side is 30 units and the neighboring side is about 52 units.
Sin30= 30/60=1/2
Cos30= 52/60= 13/15
Tan30=30/52=15/26
Cot30=52/30=26/15
The exact value of Cos30 is √3/2 as you know. However, this number does not allow us to do operations as fast as the ratio 13/15.
The result of the first one 0.86602 while the result of the second one 0.86666. This means that the value is correct up to the fourth digit after the comma. This is more than enough for the precision of the work in the time.
Now we know that we can find sine or cosine values for any angle using sine quadrant on our astrolabe’s back side. Now let’s think how can we calculate values of root numbers using sine quadrant. Sine quadrant gave us cos30 which is √3/2 or 52/60 by our astrolabe. So double amount of this will be √3:
52/60*2 = 104/60=1.7333.. Real value of √3 is 173205…. So it is precise enough.
Lets calculate other root numbers.
| √2 |
| Cos45=√2/2 |
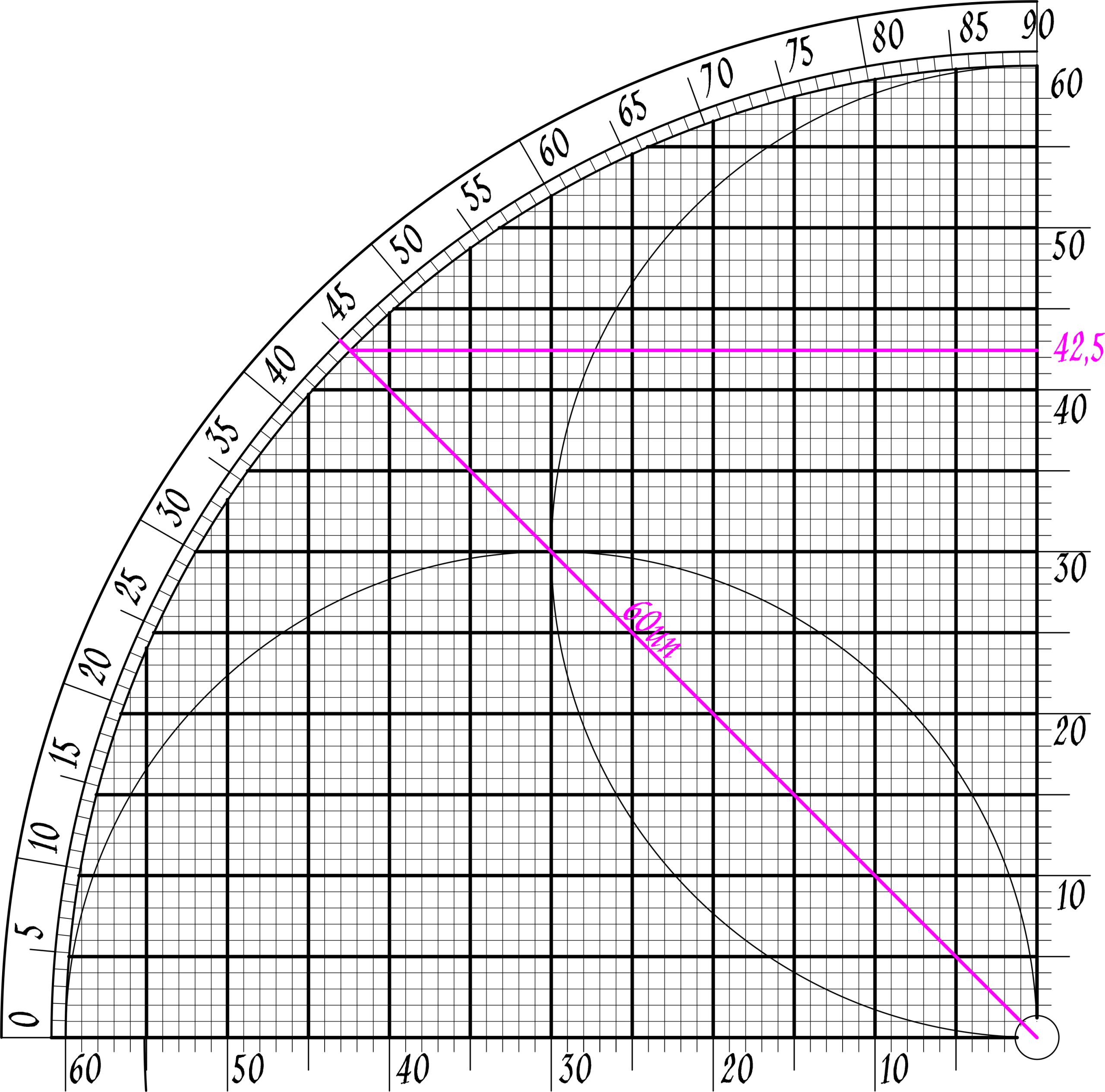 |
| Cos45:42,5/60 |
| If √2/2 = 42,5/60 √2≈85/60 = 17/12 = 1,417 √2=1,414 |
| √5 |
| We need to create a right triange which is composed of one side √5 and other sides whole numbers. |
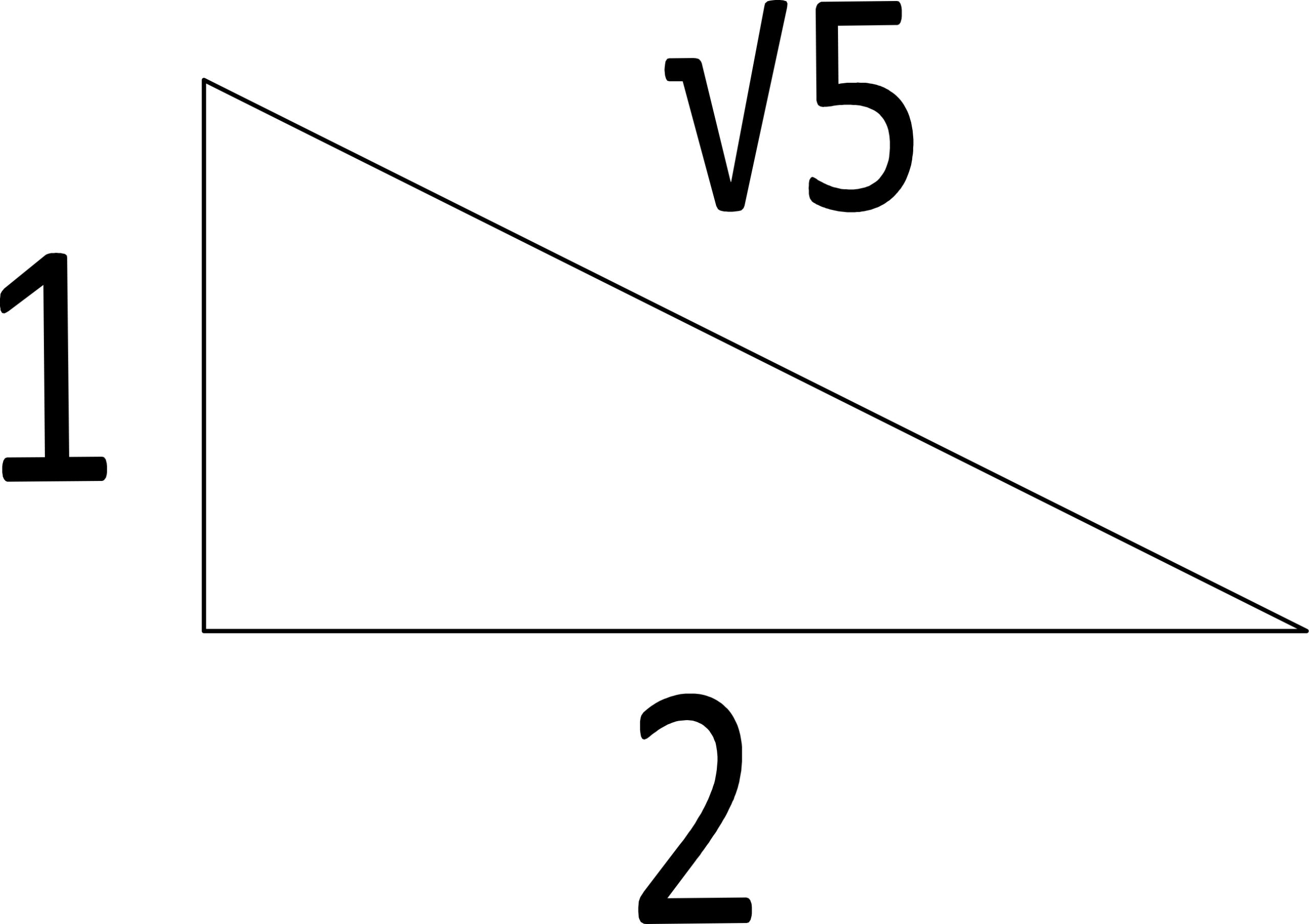 |
| cos(1-2-√5)=2/√5 |
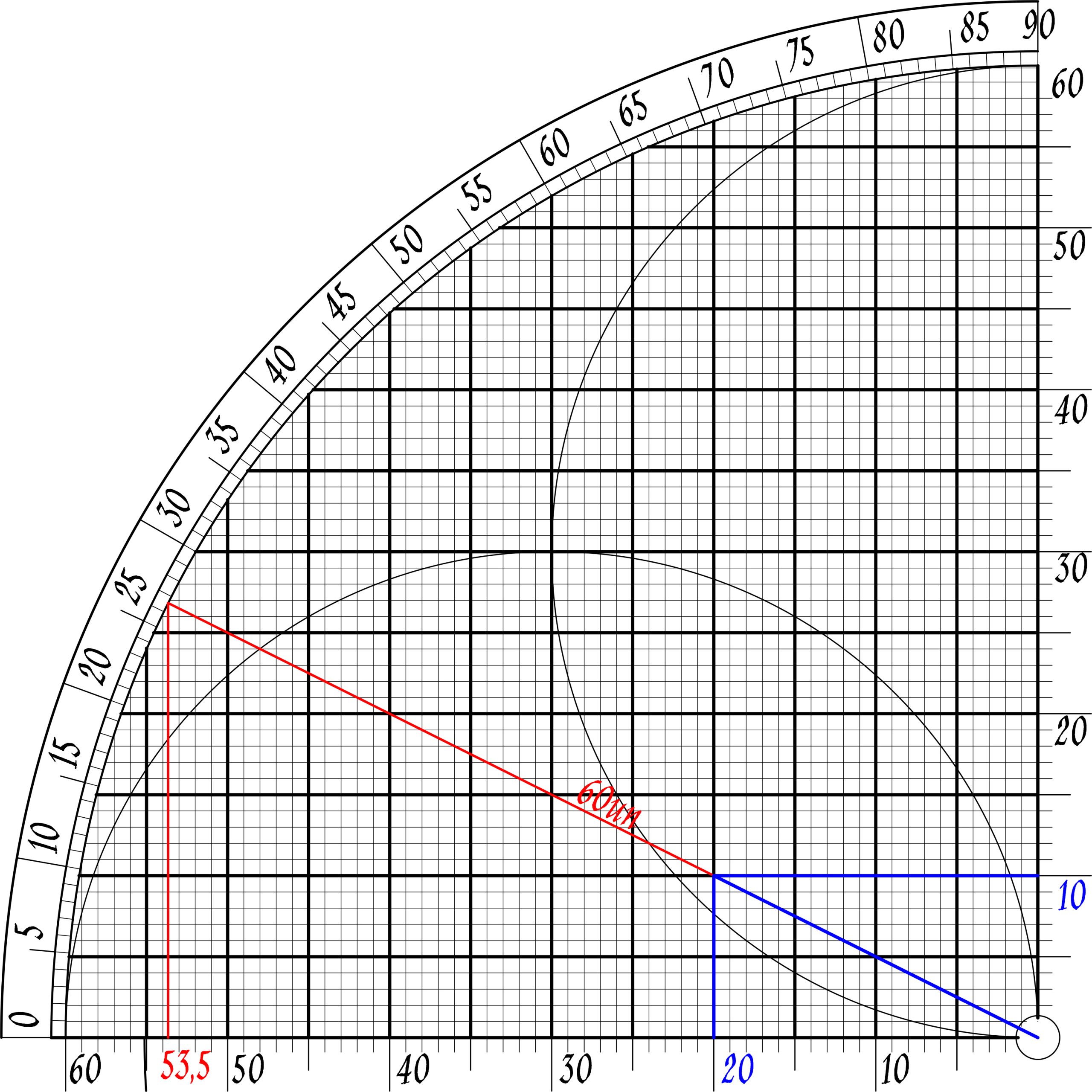 |
| 2/√5 = 53,5/60 √5/2 = 60/53,5 √5≈120/53,5 = 2,243 √5:2,236 |
| √7 |
| We need to create a right triange which is composed of one side √7 and other sides whole numbers. |
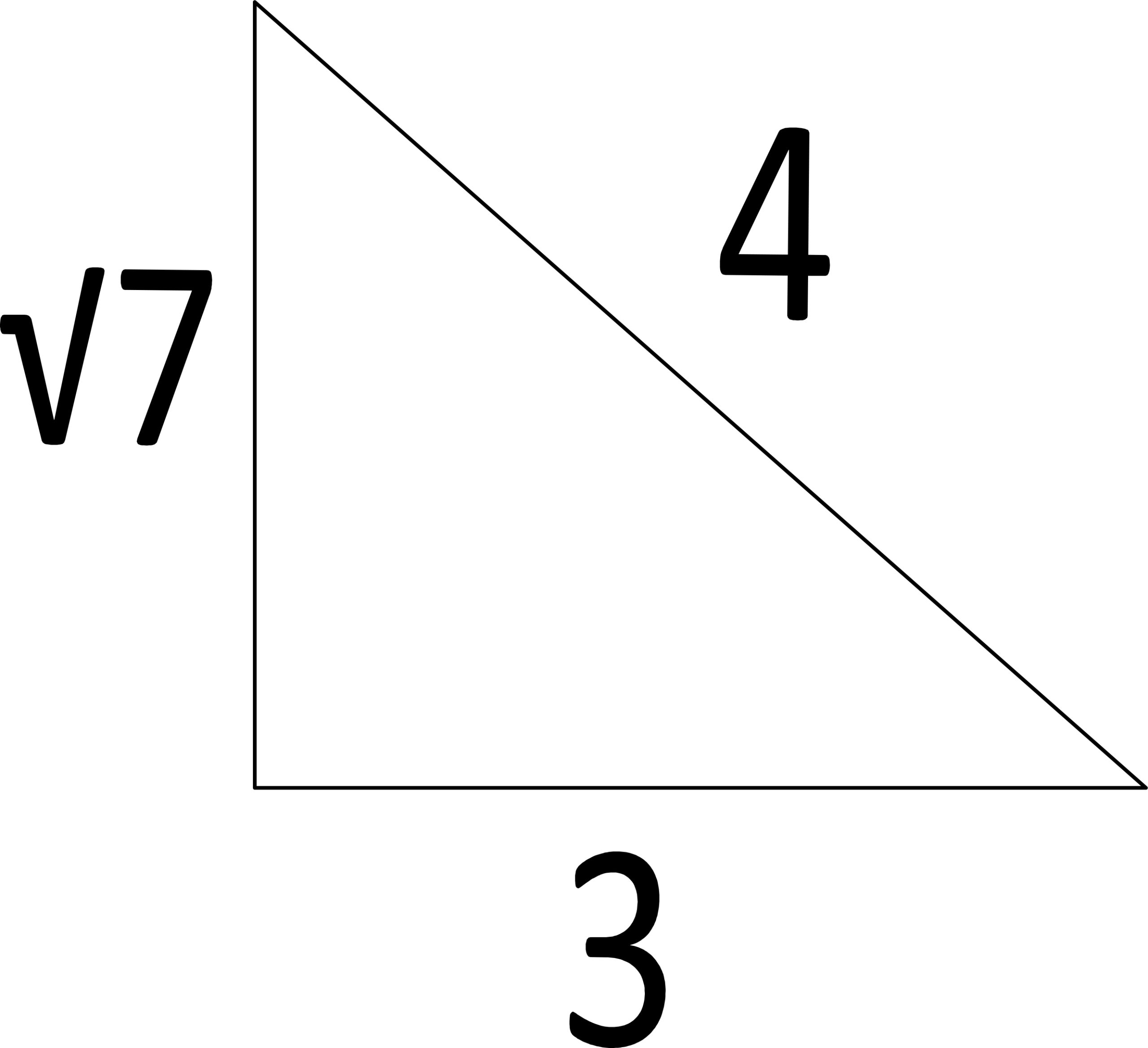 |
| 4= 60 Unit 3=45unit We create our similar triangle |
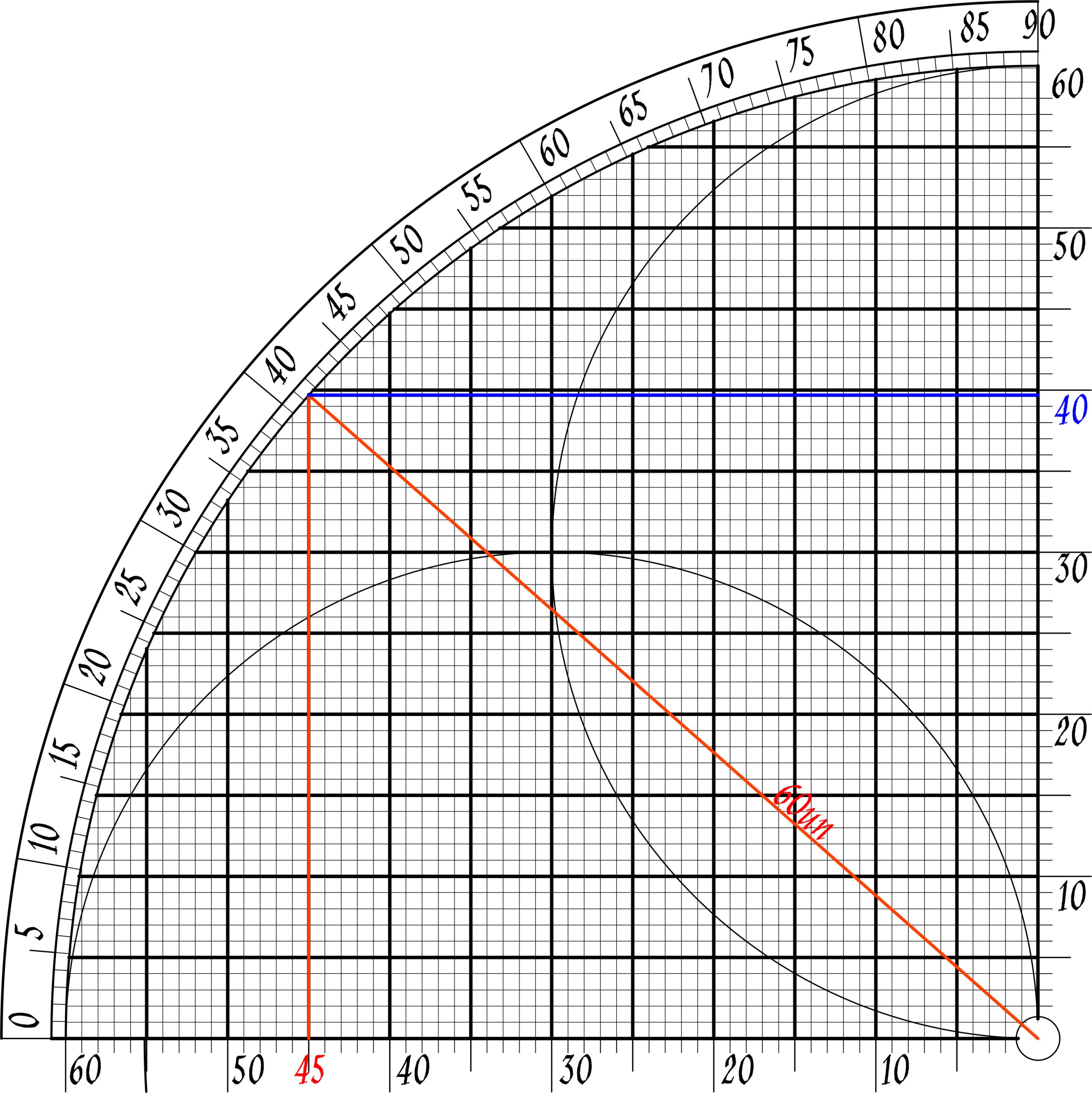 |
| sin(√7-3-4)= √7/4 ≈ 40/60=2/3 √7≈(2/3)*4 =8/3=2,667 √72,646 |
| √10 |
| We need to create a right triange which is composed of one side √10 and other sides whole numbers. |
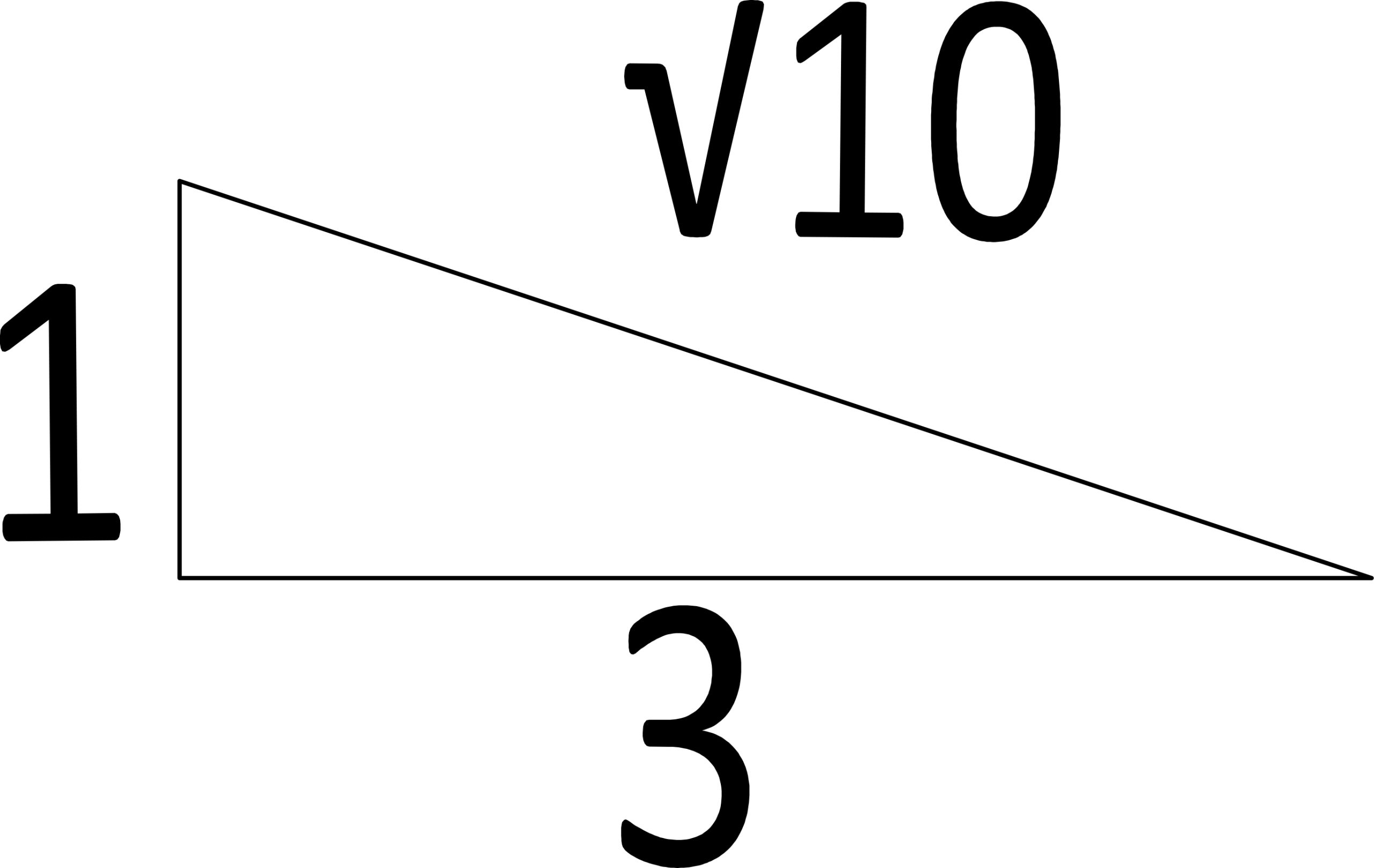 |
| We create our similar triangle |
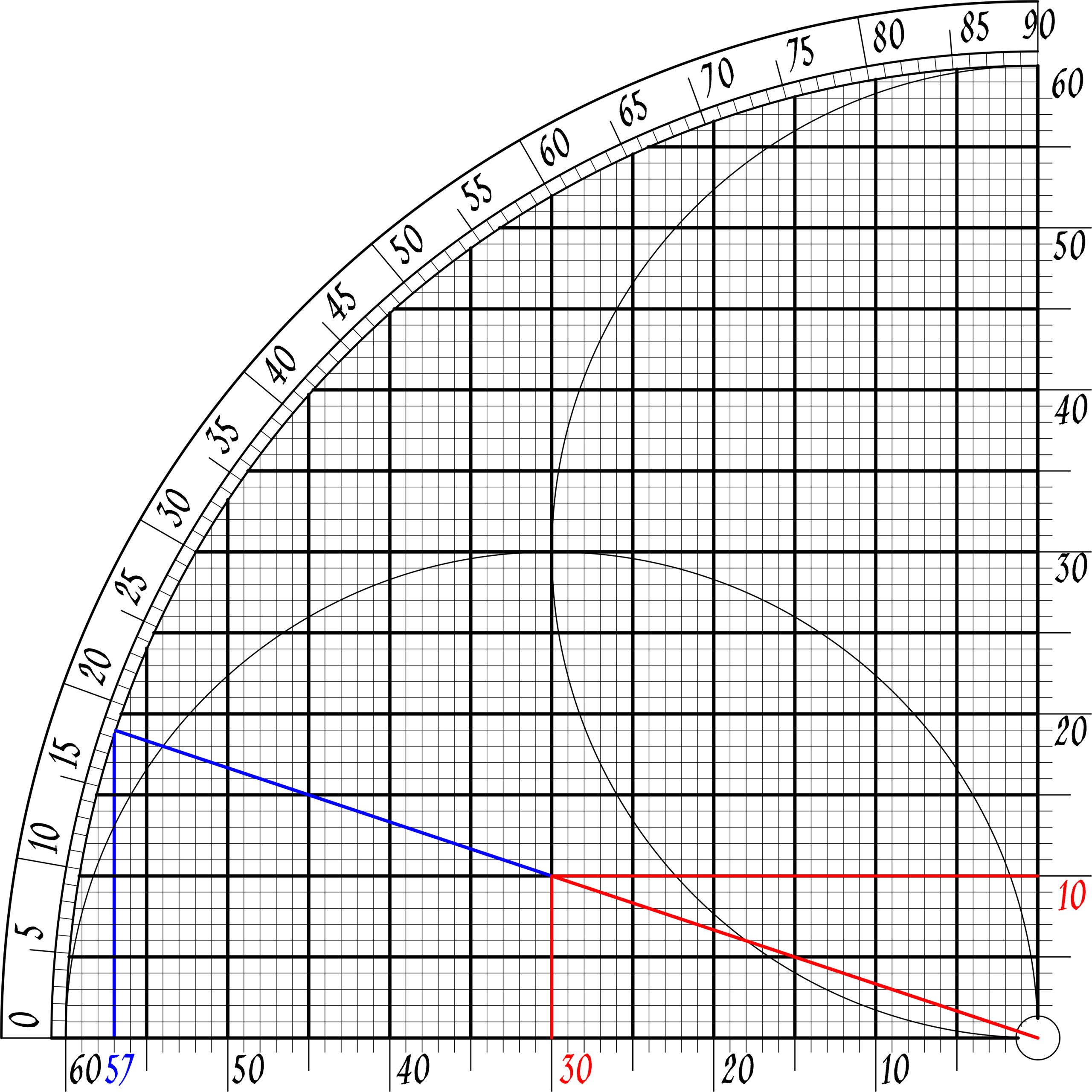 |
| cos(1-3-√10)= 3/√10≈57/60=19/20 (20/19)*3=60/19=3,158 √10=3,162 |
When we apply same method for next several prime numbers we get this table:
| Trigonometric value | Root value | Aprox. decimal Value | Astrolabe Fract.Value | Simplified value | Decimal value of astrolabe fraction | Error margin % |
| Cos45 | √2/2 | 0,707 | 42,5/60 | 0,708 | 0,2 | |
| √2 | 1,414 | 85/60 | 17/12 | 1,417 | 0,2 | |
| cos30 | √3/2 | 0,866 | 52/60=13/15 | 0,867 | 0,1 | |
| √3 | 1,732 | 104/60 | 26/15 | 1,733 | 0,1 | |
| cos(1-2-√5) | 2/√5 | 0,894 | 53,5/60 | 0,892 | 0,3 | |
| √5 | 2,236 | (60/53,5)*2 | 120/53,5 | 2,243 | 0,3 | |
| sin(√7-3-4) | √7/4 | 0,661 | 40/60=2/3 | 0,667 | 0,8 | |
| √7 | 2,646 | (40/60)*4 | 8/3 | 2,667 | 0,8 | |
| cos(1-3-√10) | 3/√10 | 0,949 | 57/60=19/20 | 0,950 | 0,1 | |
| √10 | 3,162 | (60/57)*3 | 60/19 | 3,158 | 0,1 | |
| sin(√11-5-6) | √11/6 | 0,553 | 33/60=11/20 | 0,550 | 0,5 | |
| √11 | 3,317 | (33/60)*6 | 33/10 | 3,300 | 0,5 | |
| cos(2-3-√13) | 2/√13 | 0,555 | 33/60=11/20 | 0,550 | 0,8 | |
| √13 | 3,606 | (60/33)*2 | 40/11 | 3,636 | 0,9 | |
| sin(1-4-√17) | 1/√17 | 0,243 | 14,5/60 | 0,242 | 0,4 | |
| √17 | 4,123 | 60/14,5 | 60/14,5 | 4,138 | 0,4 | |
| sin(√19-9-10) | √19/10 | 0,436 | 26/60 | 0,433 | 0,6 | |
| √19 | 4,359 | (26/60)*10=13/3 | 13/3 | 4,333 | 0,6 | |
| cos(2-√21-5) | √21/5 | 0,917 | 55/60=11/12 | 0,917 | 0,0 | |
| √21 | 4,583 | 55/12 | 55/12 | 4,583 | 0,0 | |
| sin(11-√23-12) | √23/12 | 0,400 | 24/60 | 0,400 | 0,1 | |
| √23 | 4,796 | (24/60)*12 | 24/5 | 4,800 | 0,1 | |
| sin(2-5-√29) | 2/√29 | 0,371 | 22,3/60 | 0,372 | 0,1 | |
| √29 | 5,385 | (60/22,3)*2 | 120/22,3 | 5,381 | 0,1 | |
| sin(√31-15-16) | √31/16 | 0,348 | 21/60 | 0,350 | 0,6 | |
| √31 | 5,568 | (21/60)*16 | 28/5 | 5,600 | 0,6 | |
| tan(4-√33-7) | √33/7 | 0,821 | 49/60 | 0,817 | 0,5 | |
| √33 | 5,745 | 343/60 | 34,3/6 | 5,717 | 0,5 | |
| sin(1-6-√37) | 1/√37 | 0,164 | 10/60 | 0,167 | 1,4 | |
| √37 | 6,083 | 6/1 | 6 | 6,000 | 1,4 | |
| sin(√41/20/21) | √41/21 | 0,305 | 18/60 | 0,308 | 1,1 | |
| √41 | 6,403 | (18,5/60)*21 | 129,5/20 | 6,475 | 1,1 | |
| cos(√43-21-22) | √43/22 | 0,298 | 18/60 | 0,300 | 0,6 | |
| √43 | 6,557 | (18/60)*22 | 33/5 | 6,600 | 0,6 | |
| sin(√47-23-24) | √47/24 | 0,286 | 17/60 | 0,283 | 0,8 | |
| √47 | 6,856 | (17/60)*24 | 35/5 | 6,800 | 0,8 |
As a result, astrolabe gives us aproximate values in fratcional form for all rooted numbers with error margin less than 1%, mainly less than 0,5. We can assume that this was a big facility in the times when there were no calculators to make quick calculations.
İbrahim AYBEK/Lisbon/2024





Son Yorumlar